-
- An older draft of my book “Incidence Theory” (with a focus on the polynomial method). For the published version, see here.
- Polynomial method lecture notes (with a focus on incidences). These are mostly subsumed by the above book. The main exception is a proof of the complete Guth-Katz distinct distances theorem that involves ruled surfaces and flat points.
- Chapter 1. Introduction to geometric incidences, related problems in discrete geometry, and first applications.
- Chapter 2. Some basic real algebraic geometry.
- Chapter 3. Polynomial partitioning and how to use it to obtain incidence bounds.
- Chapter 4. Constant-sized polynomial partitioning.
- Chapter 5. The joints problem.
- Chapter 6. The Elekes-Sharir-Guth-Katz
Framework. - Chapter 7. Lines in
.
- Chapter 8. Distinct intersection points (finishing the Guth-Katz distinct distances problem).
- Chapter 9. More distinct distances problems.
- Additive combinatorics lecture notes:
- The Konyagin-Shkredov sum-product bound – The proof of the sum-product bound of Konyagin and Shkredov, explained in detail.
-
- Distinct Distances: Open Problems and Current Bounds – This is my ongoing attempt to survey the many open variants of the distinct distances problem, and the best known bounds for them. Occasionally I also include proofs, if they are short and elegant.
Comments, questions, and complaints are welcome.

Pingback: The second-partitioning-polynomial technique (part 1) | Some Plane Truths
Pingback: Random Stories from IPAM – Part1 | Some Plane Truths
Pingback: Incidences in the complex plane | Some Plane Truths
Pingback: The Sum-Product Bound of Konyagin and Shkredov – Some Plane Truths
This is a minor quibble, but should Theorem 6.5 say C(d,2) + 2d + 2, and not C(d,2) + 3d + 2?
In the Incidence Theory book, that is.
Dear Anurag,
In the terms of the form , we also include that case of
, we also include that case of 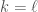 . This means that there are
. This means that there are 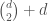 such terms. So this is not a mistake, but it might indeed be nice to add a clarification there.
such terms. So this is not a mistake, but it might indeed be nice to add a clarification there.
If you find any other issues, I’m always happy to hear about them. It’s better to email me than to write about it here.
Ahh fair, thanks for the clarification! I do have some more comments/questions on that section, I’ll write you a mail when I get some time.