Since my previous post, I moved from freezing New York to sunny LA. I am participating in a semester on Algebraic Techniques for Combinatorial and Computational Geometry, at the IPAM institute. The lack of posts on the blog in the past several weeks is due to the constant activities and the large number of interesting people to interact with. This post contains some random stories from my stay at IPAM.
During pie day (March 14th), all of the food served in IPAM was round.
So far the main events were a week of tutorials and another week consisting of a workshop about “Combinatorial Geometry Problems at the Algebraic Interface”. These contained many interesting talks, which were also videotaped. Once the videos will be online, I will post a link in the blog. Here I only mention one talk which gave me quite a surprise – Larry Guth‘s talk.
At the beginning of his talk, Larry stated that he will present a significantly simpler variant of part the distinct distances proof (the one by Katz and himself). You might remember that, using the Elekes-Sharir framework, the distinct distances problem is reduced to a point-line incidences problem in 
: Given a set of 
lines, such that every point is incident to at most 
of the lines and that every plane and regulus contain at most of the lines, what is the maximum number of points that can be incident to at least 
of the lines (where 
). Larry’s new technique proves the following slightly weaker incidences bound.
: Given a set of 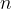lines, such that every point is incident to at most of the lines and that every plane and regulus contain at most of the lines, what is the maximum number of points that can be incident to at least 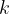of the lines (where ). Larry’s new technique proves the following slightly weaker incidences bound. Theorem (Guth `14). Consider a set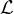 
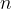of lines in , so that any surface of degree at most 
(a constant that depends only on 
) contains at most 
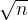lines of 
. Then for any 
and 
, the number of points of that are contained in at least 
lines of is 
of lines in , so that any surface of degree at most (a constant that depends only on ) contains at most lines of . Then for any and , the number of points of that are contained in at least lines of is The surprising part is that the new proof was based on constant sized partitioning polynomials (on which I plan to write a couple of expository posts, as part of my expository series about the polynomial method). When using such polynomials for problems of this sort, one encounters a difficultly. It is hard to describe this difficulty without first explaining the technique, but my impression is that this difficulty was the main issue in various other recent incidences-related projects, and that now we might see various other works that rely on Larry’s technique. In his talk, Larry also mentioned that this technique can work for other types of curves, which immediately implies a series of improved point-curve incidence bounds in .
. 
A talk by Tao in IPAM. How many of the mathematicians in the audience can you recognize?
And for something completely different: I had an issue with my visa, and was told that I should exit and reenter the country. This resulted in a 13-hour bus trip to Tijuana and back to LA. My only souvenir from this trip is the following picture of a pharmacy for people that are waiting in line to enter the US. I wonder sort of things people buy at a pharmacy while waiting to go through immigration…
There’s a lot more to tell, so more IPAM stories later on.
Some Plane Truths 
Pingback: Random Stories from IPAM – Part 2 | Some Plane Truths