Point Sets with Few Distinct Distances

Ben Lund and I were sitting in a small Korean restaurant and discussing an old conjecture of Erdős. Erdős suggested that if a set of 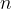points in 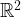spans distinct distances, then the vertices of this set must span either a square or an equilateral triangle. Presumably, this conjecture was made because the two best-known examples of sets with distinct distances are subsets of the integer lattice and of the triangular lattice. (By the triangular lattice, I mean the vertices of a tiling of the plane with equilateral triangles.)

A subset of the integer lattice and a subset of the triangular lattice.

A subset of the integer lattice spans many squares and no equilateral triangles, while a subset of the triangular lattice spans many equilateral triangles and no squares. We can create various similar configurations by taking one of these two configurations and then applying rotations, uniform scaling, and taking subsets. Such configurations still contain squares or equilateral triangles. Ben and I were wondering whether we can find additional configurations, which are not “related” to the integer lattice or to the triangular lattice. Surprisingly, we managed to find a large family of other configurations. Moreover, many of these configurations do not span any squares or triangles, disproving Erdős’ conjecture. We then discovered that these configurations were already known, and appeared in a paper by Moree and Osburn. I guess that this is another case of lack of communication between different mathematical communities…

Incidences: Lower Bounds (part 2)

This is the second in my series of posts concerning lower bound for incidence problems (see the first post here). This post describes Elekes’ point-line construction, which is quite different from Erdős’ construction, although it yields asymptotically the same number of incidences. While preparing this post, I was quite surprised to discover that this construction yields constants better than those that are stated as the best known ones (e.g., in the research problems book).

Update 1 (11/26/2014): Frank the Zeeuw pointed out that this bound was already noticed in Section 1.1 of Roel Apfelbaum’s Ph.D. dissertation.

Update 2 (01/01/2018): It was pointed in this paper by Balko, Cibulka, and Valtr that the analysis of Pach and Tóth leads to the much better constant 1.27. This stronger bound is not stated in that paper due to a miscalculation.

György Elekes.

Elekes’ construction is simpler and more elementary, in the sense that it only requires basic counting techniques (unlike Erdős’ construction which also relies on some number theory). As we shall see in the following posts, it is also easier to generalize to other types of planar curves. Moreover, unless I have some mistake, it seems to lead to better constants. Specifically, given points and lines in the plane, the maximum number of incidences, as shown by Pach and Tóth, is at least . In various places (such as the aforementioned open problems book) this is stated as the best known lower bound. The best known upper bound, obtained by combining a technique from the same paper of Pach and Tóth with a recent improvement by Ackerman, is about . Elekes’ construction leads to the improved lower bound .

In both constructions the point set is a subset of the integer lattice. However, Erdős’ construction is based on a square lattice (i.e., of size ), while Elekes’ contruction is a rather uneven lattice (except for the extreme case when ).