In this post I briefly mention several recent papers that are related to the topics of this blog (I might later write more detailed posts about some of these). This is not a comprehensive list, as there are many new relevant papers. Some other recent results can be found in the list of papers that were accepted to SoCG 2014, though I am not mentioning papers that still do not have a full version available online. Soon I will also add these to the related papers page.
1. Polynomials vanishing on grids: The Elekes-Rónyai problem revisited / Raz, Sharir, and Solymosi. In my previous post, about the partial Elekes-Sharir framework, I mentioned the existence of a couple of unpublished results that apply this technique to problems that do not directly involve distinct distances. This is the first of these papers, and the main result in it is the following improvement of a special case of recent result by Elekes and Szabó.
Theorem 1 (Raz, Sharir, and Solymosi). Consider a grid 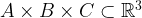 , where
, where 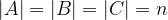 , and a polynomial
, and a polynomial ![f\in{\mathbb R}[x,y,z]](https://s0.wp.com/latex.php?latex=f%5Cin%7B%5Cmathbb+R%7D%5Bx%2Cy%2Cz%5D++&bg=ffffff&fg=000000&s=1&c=20201002) which is of the form
which is of the form 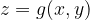 . Then if
. Then if 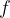 vanishes on
vanishes on 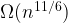 points of the grid, it must be either of the form
points of the grid, it must be either of the form  or the form
or the form  , for
, for ![h,\varphi,\psi \in {\mathbb R}[x]](https://s0.wp.com/latex.php?latex=h%2C%5Cvarphi%2C%5Cpsi+%5Cin+%7B%5Cmathbb+R%7D%5Bx%5D++&bg=ffffff&fg=000000&s=1&c=20201002) .
.
This appears to be a rather strong result with various applications, including subsuming several previous results that were obtained by applying the partial Elekes-Sharir framework. The paper by Elekes and Szabó is significantly more general in the sense that it applies to any 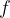 (not just of the form
(not just of the form  ), to grids in the complex space, and to more general scenarios in higher dimensions. However, it is not clear to me (or to other people that I have asked) what exactly are the bounds that were obtained in it (that is, compared to
), to grids in the complex space, and to more general scenarios in higher dimensions. However, it is not clear to me (or to other people that I have asked) what exactly are the bounds that were obtained in it (that is, compared to 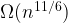 ), which seem to also depend on the degree of
), which seem to also depend on the degree of 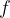 .
.
2. Distinct volume subsets / Conlon, Fox, Gasarch, Harris, Ulrich, and Zbarsky. I already had a post about a previous version of this paper (which back then I found through google scholar and by mistake thought that it was public). In one rather imprecise sentence: the paper shows that for every set 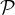 of
of 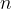 points in
points in  and for every
and for every  , there exists a large subset
, there exists a large subset 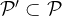 , such the points of
, such the points of 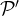 do not span two
do not span two  -dimensional simplices with the same volume (hence the name Distinct volume subsets). The main results have remained more or less the same and you can find more details about them in my original post. However, the new (and official!) version of the paper is significantly shorter. As William Gasarch was describing it to me, the new version has “cleaner defintions, cleaner proofs, and more precise results.”
-dimensional simplices with the same volume (hence the name Distinct volume subsets). The main results have remained more or less the same and you can find more details about them in my original post. However, the new (and official!) version of the paper is significantly shorter. As William Gasarch was describing it to me, the new version has “cleaner defintions, cleaner proofs, and more precise results.”
3. Algebraic combinatorial geometry: the polynomial method in arithmetic combinatorics, incidence combinatorics, and number theory / Tao. This paper is a survey and is already three months old, but I think that it is worth mentioning. The survey discusses recent techniques such as polynomial partitioning, the existence of bounded-degree polynomials that vanish over a given point set, etc., but also other topics such as Alon’s combinatorial nullstellensatz.
In the survey, Tao dubs this (sub-)field as algebraic combinatorial geometry, so perhaps I should start saying that this is a blog that focuses on algebraic combinatorial geometry. I am quite happy about Tao uniting these various techniques under one roof and naming it. I hope that this would help making the field more known and to push it forward.
