I recently attended a wonderful workshop about
Algebraic methods in combinatorics, which took place in Harvard’s
CMSA. There were many interesting participants from a variety of combinatorial fields, and a very friendly/productive atmosphere. My talk focused on a
recent work with Cosmin Pohoata, and I also mentioned some distinct distances result that we derived. During the talk
Zeev Dvir asked about an additive variant of the problem. After thinking about this variant for a bit, I think that it is a natural interesting problem. Surprisingly, so far I did not manage to find any hint of previous work on it (this might say more about my search capabilities than about the problem…)

 Zeev Dvir and Cosmin Pohoata.
Zeev Dvir and Cosmin Pohoata.Let

denote the minimum size

can have, when

is a set of
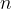
real numbers with the property that for any
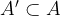
with

we have

. That is, by having a local additive property of every small subset, we wish to obtain a global additive property of the entire set. For simplicity, we will ignore zero in the difference set. Similarly, we will ignore negative differences. These assumptions do not change the problem, but make it easier to discuss.
As a first example, note that

is the minimum number of differences determined by a set of
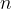
reals with no 3-term arithmetic progressions.
Behrend’s construction is a set

of positive integers
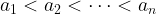
with no 3-term arithmetic progression and

. Thus,

.
For another simple example, Consider a constant
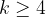
. Since we consider only positive differences, any set of
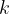
reals determines at most

differences. If a specific difference

repeats
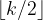
times, then by taking the numbers that span

we obtain

such that

and
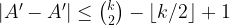
. Thus, by asking every subset of size
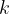
to span at least

differences, we obtain that no difference repeats
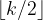
times in

. In other words
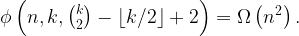

That is, when moving from
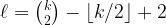
to
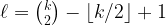
, we move from a trivial problem to a wide open one. My work with Cosmin Pohoata leads to the following result.
Theorem 1. For any  there exists
there exists  such that
such that

For example, when

we get the bound
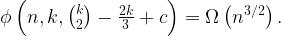
When

we get a significant improvement for the range of the Erdős-Gyárfás bound:
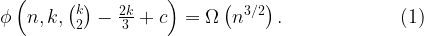
Since not much is known for this problem, it seems plausible that additional bounds could be obtained using current tools. Our technique does not rely on any additive properties, and holds for a more abstract scenario of graphs with colored edges. Hopefully in the case of difference sets one would be able to use additive properties to improve the bounds. Moreover, so far I know nothing about much smaller values of
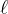
, such as

.
Proof sketch for Theorem 1. For simplicity, let us consider the case of

, as stated in
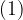
. Other values of

are handled in a similar manner. Let

be a set of
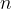
reals, such that any

of size
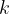
satisfies
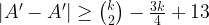
. We define the
third distance energy of

as
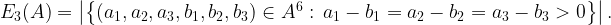
The proof is based on double counting

. For

, let
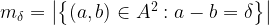
. That is,

is the number of representations of

as a difference of two elements of

. Note that the number of 6-tuples that satisfy

is

. A simple application of Hölder ‘s inequality implies
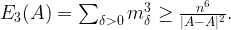
To obtain a lower bound for
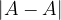
, it remains to derive an upper bound for

.
For
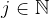
let

denote the number of differences

such that
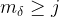
. A dyadic decomposition gives
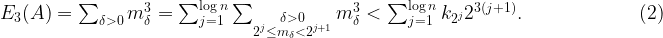
For
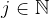
let
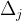
denote the set of
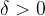
with

(so

). For
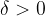
, let

be the set of points that participate in at least one of the representations of

. If there exist
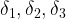
such that

, then there exist a subset

with

and

(see
the paper for a full explanation). Thus, for every
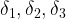
we have that

.
We have

sets

with
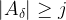
. These are all subsets of the same set

of size
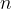
, and every three intersect in fewer than

elements. We now have a set theoretic problem: How many large subsets can

have with no three having a large intersection. We can use the following counting lemma (for example, see Lemma 2.3 of
Jukna’s Extremal Combinatorics) to obtain an upper bound on

.
Lemma 2. Let  be a set of
be a set of 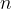 elements and let
elements and let  be an integer. Let
be an integer. Let 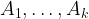 be subsets of
be subsets of  , each of size at least
, each of size at least 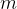 . If
. If  then there exist
then there exist  such that
such that  .
.
Lemma 2 implies the bound

for large values of

. Combining this with
and with a couple of standard arguments leads to

. Combining this with

implies

.
. Let
be a set of
real numbers. How large can the multiplicative energy
be?
must be asymptotically smaller than
?
for which
is asymptotically larger than
?
. Sub-polynomial improvements would be less interesting. Multiplicative energy means

is larger. Let
, where
.
. The Cauchy-Schwarz inequality implies that
, up to sub-polynomial factors. This implies that
, up to sub-polynomial factors. In this case, the trivial upper bound is
.
and the upper bound
, up to sub-polynomial factors.




