This post is about another new distinct distances result, which was just uploaded to arXiv. It is a paper by Zahl, de Zeeuw, and myself.
Let us start by asking what are currently the main challenges in studying distinct distances (you’re welcome to share your thoughts about this in the comments). It seems to me that most people consider the main challenge to be the  -dimensional variant of the distinct distances problem (see the second half of this post for more details). I would like to suggest that another main problem is characterizing the point sets that determine a small number of distinct distances.
-dimensional variant of the distinct distances problem (see the second half of this post for more details). I would like to suggest that another main problem is characterizing the point sets that determine a small number of distinct distances.
I already wrote about the characterization problem in this post, and I will now repeat a few sentences from there. So far, all the known point sets that determine a sublinear number of distinct distances are  lattices, possibly with some minor changes. For example, any
lattices, possibly with some minor changes. For example, any  subset of the integer lattice determines
subset of the integer lattice determines  distinct distances, and so does a
distinct distances, and so does a  subset of the following triangular lattice:
subset of the following triangular lattice:
Over 25 years ago Erdős asked whether every point set that determines  distinct distances “has lattice structure”. However, even after so many years and Guth and Katz’s breakthrough, we still hardly know anything about this problem. A proof by Szemerédi (unpublished and originally described in a 1975 paper by Erdős) implies that for every
distinct distances “has lattice structure”. However, even after so many years and Guth and Katz’s breakthrough, we still hardly know anything about this problem. A proof by Szemerédi (unpublished and originally described in a 1975 paper by Erdős) implies that for every 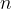 -point set
-point set 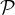 , there exists a line
, there exists a line 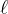 that contains
that contains  points of
points of 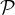 . It had been conjectured by Erdős that this bound can be improved to
. It had been conjectured by Erdős that this bound can be improved to  , though no improvement had been discovered in the decades that passed. It is an interesting challenge to prove even the case of
, though no improvement had been discovered in the decades that passed. It is an interesting challenge to prove even the case of  points on a line.
points on a line.
In the new paper, we study the “complementary” problem of proving that there must not be a line with too many points on it.
Theorem 1. (S’, Zahl, and de Zeeuw) Let 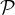 be a set of
be a set of 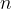 points that determine
points that determine  distinct distances. Then no line contains
distinct distances. Then no line contains 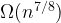 points of
points of 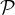 .
.