The Sum-Product Bound of Konyagin and Shkredov

In Solymosi’s famous 2009 paper, he proved that every finite set 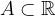satisfies

In the past couple of years, Konyagin and Shkredov published two papers that extend Solymosi’s argument, obtaining a slightly stronger sum-product bound (one and two). These papers derive several additional results, and apply a variety of tools. I just uploaded to this blog my own exposition to the sum-product proof of Konyagin and Shkredov (a link can also be found in the pdf files page). This exposition ignores the additional results that are in the two papers, and tries to explain in detail every step that is part of the sum-product proof. In this aspect, the document would hopefully also fit beginners. As usual, I’m happy to receive any comments and corrections.

Ilya Shkredov and Sergei Konyagin.