Incidences Outside of Discrete Geometry

Starting the 1980’s, more and more applications of geometric incidences have been found in discrete geometry. By now, one can arguably claim that there are countless such applications. More surprising are the applications of incidences outside of discrete geometry. In the past decade such applications have been discovered in harmonic analysis, theoretical computer science, number theory, and more. This post is my attempt to list these applications. If you are familiar with additional applications that I did not include, I’d be very interested to hear about them (in the comments below or by email).

Additive combinatorics: One of the main milestones in the study of the sum-product problem is a seminal paper by Elekes, in which he reduced the problem to a point-line incidence problem in 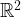. This led to a variety of results in additive combinatorics that rely on incidences. Tao and Vu’s additive combinatorics book contains a full chapter that is dedicated to incidences. Konyagin and Shkredov’s recent improvement of the sum-product bound also relies indirectly on incidences (to bound the number of collinear triples in a lattice). For more examples, see here and here. Also, several additive combinatorics results in finite fields rely on incidence bounds in finite fields (e.g., see this paper).

Fourier restriction problems: Bourgain and Demeter rely on incidences to derive bounds for the discrete Fourier restriction to the four and five dimensional spheres. Incidences also appear in several related papers by the same authors (e.g., see here and here).

Number theory: A recent paper of Bombieri and Bourgain studies a type of additive energy of the Gaussian integers by relying on incidences with unit circles in .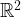

Error correcting codes: A family of papers by Dvir, Saraf, Wigderson, and others use incidences to study error correcting codes. For example, see this paper and this paper. These papers rely mainly on Sylvester-Gallai problems, which do not exactly fit the standard incidence problem formulation. Still, the authors of these paper and others consider these as proper incidence problems.

Extractors: Yet another novel use of incidences by Jean Bourgain. Bourgain relied on a finite field point-line incidence bound to build 2-source extractors. Recently this result has been superseded, as far as I understand without relying on incidences in any way.

Minors of totally positive matrices: Farber, Ray, and Smorodinsky used incidences to bound the number of times that a minor can repeat in a totally positive matrix.

It might also be interesting to state results that do not rely on incidences but do rely on the same polynomial partitioning technique (applied in the same way):

More restriction problems: Guth recently relied on polynomial partitioning to derive improved restriction estimates for smooth compact surface in with strictly positive second fundamental form.

Range searching algorithms: Agarwal, Matoušek,and Sharir used polynomial partitioning to derive range searching algorithms for semialgebraic sets. A later simplification of this result, also based on polynomial partitioning, was derived by Matoušek and Patáková.

Any comments, corrections, and additions to the above list are welcome.